Granulometry (morphology)

In mathematical morphology, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening operations. It was introduced by Georges Matheron in the 1960s, and is the basis for the characterization of the concept of size in mathematical morphology.

Granulometry generated by a structuring element

Let B be a structuring element in an Euclidean space or grid E, and consider the family 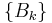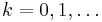$\{B_k\}$ , $k=0,1,\ldots$ , given by:

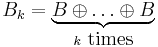$B_k=\underbrace{B\oplus\ldots\oplus B}_{k\mbox{ times}}$ ,

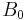where $\oplus$ denotes morphological dilation. By convention, $B_0$ is the set containing only the origin of E, and $B_1=B$ .

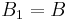Let X be a set (i.e., a binary image in mathematical morphology), and consider the series of sets 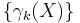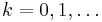$\{\gamma_k(X)\}$ , $k=0,1,\ldots$ , given by:

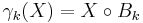$\gamma_k(X)=X\circ B_k$ ,

where 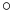$\circ$ denotes the morphological opening.

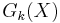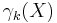The granulometry function $G_k(X)$ is the cardinality (i.e., area or volume, in continuous Euclidean space, or number of elements, in grids) of the image $\gamma_k(X)$ :

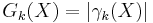$G_k(X)=|\gamma_k(X)|$ .

The pattern spectrum or size distribution of X is the collection of sets 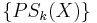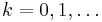$\{PS_k(X)\}$ , $k=0,1,\ldots$ , given by:

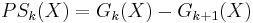$PS_k(X) = G_{k}(X)-G_{k%2B1}(X)$ .

The parameter k is referred to as size, and the component k of the pattern spectrum 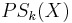$PS_k(X)$ provides a rough estimate for the amount of grains of size k in the image X. Peaks of 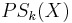$PS_k(X)$ indicate relatively large quantities of grains of the corresponding sizes.

Sieving axioms

The above common method is a particular case of the more general approach derived by Matheron.

The French mathematician was inspired by sieving as a means of characterizing size. In sieving, a granular sample is worked through a series of sieves with decreasing hole sizes. As a consequence, the different grains in the sample are separated according to their sizes.

The operation of passing a sample through a sieve of certain hole size "k" can be mathematically described as an operator 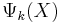$\Psi_k(X)$ that returns the subset of elements in X with sizes that are smaller or equal to k. This family of operators satisfy the following properties:

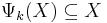Anti-extensivity: Each sieve reduces the amount of grains, i.e., $\Psi_k(X)\subseteq X$ ,
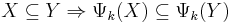Increasingness: The result of sieving a subset of a sample is a subset of the sieving of that sample, i.e., $X\subseteq Y\Rightarrow\Psi_k(X)\subseteq\Psi_k(Y)$ ,
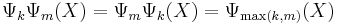"Stability": The result of passing through two sieves is determined by the sieve with smallest hole size. I.e., $\Psi_k\Psi_m(X)=\Psi_m\Psi_k(X)=\Psi_{\max(k,m)}(X)$ .

A granulometry-generating family of operators should satisfy the above three axioms.

In the above case (granulometry generated by a structuring element), 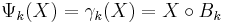$\Psi_k(X)=\gamma_k(X)=X\circ B_k$ .

Another example of granulometry-generating family is when 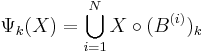$\Psi_k(X)=\bigcup_{i=1}^{N} X\circ (B^{(i)})_k$ , where 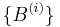$\{B^{(i)}\}$ is a set of linear structuring elements with different directions.

References

Random Sets and Integral Geometry, by Georges Matheron, Wiley 1975, ISBN 0471576212.
Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0126372403 (1982)
An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)
Morphological Image Analysis; Principles and Applications by Pierre Soille, ISBN 3540-65671-5 (1999)